今天來分享一下圖,這是一種比較復(fù)雜的非線性數(shù)據(jù)結(jié)構(gòu),之所以復(fù)雜是因為他們的數(shù)據(jù)元素之間的關(guān)系是任意的,而不像樹那樣 被幾個性質(zhì)定理框住了,元素之間的關(guān)系還是比較明顯的,圖的使用范圍很廣的,比如網(wǎng)絡(luò)爬蟲,求最短路徑等等,不過大家也不要膽怯,
越是復(fù)雜的東西越能體現(xiàn)我們碼農(nóng)的核心競爭力。
既然要學(xué)習(xí)圖,得要遵守一下圖的游戲規(guī)則。
一: 概念
圖是由“頂點”的集合和“邊”的集合組成。記作:G=(V,E);
1> 無向圖
就是“圖”中的邊沒有方向,那么(V1,V2)這條邊自然跟(V2,V1)是等價的,無向圖的表示一般用”圓括號“。
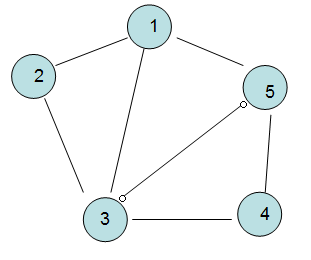
2> 有向圖
“圖“中的邊有方向,自然V1,V2>這條邊跟V2,V1>不是等價的,有向圖的表示一般用"尖括號"表示。
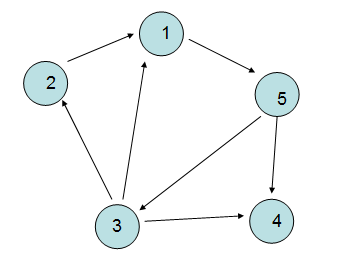
3> 鄰接點
一條邊上的兩個頂點叫做鄰接點,比如(V1,V2),(V1,V3),(V1,V5),只是在有向圖中有一個“入邊,出邊“的
概念,比如V3的入邊為V5,V3的出邊為V2,V1,V4。
4> 頂點的度
這個跟“樹”中的度的意思一樣。不過有向圖中也分為“入度”和“出度”兩種,這個相信大家懂的。
5> 完全圖
每兩個頂點都存在一條邊,這是一種完美的表現(xiàn),自然可以求出邊的數(shù)量。
無向圖:edges=n(n-1)/2;
有向圖:edges=n(n-1); //因為有向圖是有邊的,所以必須在原來的基礎(chǔ)上"X2"。
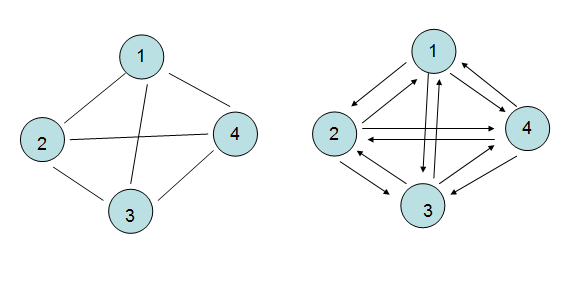
6> 子圖
如果G1的所有頂點和邊都在G2中,則G1是G2的子圖,具體不說了。
7> 路徑,路徑長度和回路(這些概念還是比較重要的)
路徑: 如果Vm到Vn之間存在一個頂點序列。則表示Vm到Vn是一條路徑。
路徑長度: 一條路徑中“邊的數(shù)量”。
簡單路徑: 若一條路徑上頂點不重復(fù)出現(xiàn),則是簡單路徑。
回路: 若路徑的第一個頂點和最后一個頂點相同,則是回路。
簡單回路: 第一個頂點和最后一個頂點相同,其它各頂點都不重復(fù)的回路則是簡單回路。
8> 連通圖和連通分量(針對無向圖而言的)
連通圖: 無向圖中,任意兩個頂點都是連通的則是連通圖,比如V1,V2,V4之間。
連通分量: 無向圖的極大連通子圖就是連通分量,一般”連通分量“就是”圖“本身,除非是“非連通圖”,
如下圖就是兩個連通分量。
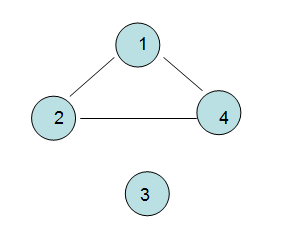
9> 強連通圖和強連通分量(針對有向圖而言)
這里主要注意的是“方向性“,V4可以到V3,但是V3無法到V4,所以不能稱為強連通圖。
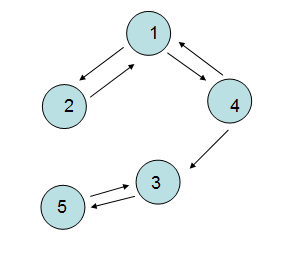
10> 網(wǎng)
邊上帶有”權(quán)值“的圖被稱為網(wǎng)。很有意思啊,呵呵。
二:存儲
圖的存儲常用的是”鄰接矩陣”和“鄰接表”。
鄰接矩陣: 手法是采用兩個數(shù)組,一個一維數(shù)組用來保存頂點信息,一個二維數(shù)組來用保存邊的信息,
缺點就是比較耗費空間。
鄰接表: 改進后的“鄰接矩陣”,缺點是不方便判斷兩個頂點之間是否有邊,但是相比節(jié)省空間。
三: 創(chuàng)建圖
這里我們就用鄰接矩陣來保存圖,一般的操作也就是:①創(chuàng)建,②遍歷
復(fù)制代碼 代碼如下:
#region 鄰接矩陣的結(jié)構(gòu)圖
/// summary>
/// 鄰接矩陣的結(jié)構(gòu)圖
/// /summary>
public class MatrixGraph
{
//保存頂點信息
public string[] vertex;
//保存邊信息
public int[,] edges;
//深搜和廣搜的遍歷標(biāo)志
public bool[] isTrav;
//頂點數(shù)量
public int vertexNum;
//邊數(shù)量
public int edgeNum;
//圖類型
public int graphType;
/// summary>
/// 存儲容量的初始化
/// /summary>
/// param name="vertexNum">/param>
/// param name="edgeNum">/param>
/// param name="graphType">/param>
public MatrixGraph(int vertexNum, int edgeNum, int graphType)
{
this.vertexNum = vertexNum;
this.edgeNum = edgeNum;
this.graphType = graphType;
vertex = new string[vertexNum];
edges = new int[vertexNum, vertexNum];
isTrav = new bool[vertexNum];
}
}
#endregion
1> 創(chuàng)建圖很簡單,讓用戶輸入一些“邊,點,權(quán)值"來構(gòu)建一下圖
復(fù)制代碼 代碼如下:
#region 圖的創(chuàng)建
/// summary>
/// 圖的創(chuàng)建
/// /summary>
/// param name="g">/param>
public MatrixGraph CreateMatrixGraph()
{
Console.WriteLine("請輸入創(chuàng)建圖的頂點個數(shù),邊個數(shù),是否為無向圖(0,1來表示),已逗號隔開。");
var initData = Console.ReadLine().Split(',').Select(i => int.Parse(i)).ToList();
MatrixGraph graph = new MatrixGraph(initData[0], initData[1], initData[2]);
Console.WriteLine("請輸入各頂點信息:");
for (int i = 0; i graph.vertexNum; i++)
{
Console.Write("\n第" + (i + 1) + "個頂點為:");
var single = Console.ReadLine();
//頂點信息加入集合中
graph.vertex[i] = single;
}
Console.WriteLine("\n請輸入構(gòu)成兩個頂點的邊和權(quán)值,以逗號隔開。\n");
for (int i = 0; i graph.edgeNum; i++)
{
Console.Write("第" + (i + 1) + "條邊:\t");
initData = Console.ReadLine().Split(',').Select(j => int.Parse(j)).ToList();
int start = initData[0];
int end = initData[1];
int weight = initData[2];
//給矩陣指定坐標(biāo)位置賦值
graph.edges[start - 1, end - 1] = weight;
//如果是無向圖,則數(shù)據(jù)呈“二,四”象限對稱
if (graph.graphType == 1)
{
graph.edges[end - 1, start - 1] = weight;
}
}
return graph;
}
#endregion
2>廣度優(yōu)先
針對下面的“圖型結(jié)構(gòu)”,我們?nèi)绾螐V度優(yōu)先呢?其實我們只要深刻理解"廣搜“給我們定義的條條框框就行了。 為了避免同一個頂點在遍歷時被多
次訪問,可以將”頂點的下標(biāo)”存放在sTrav[]的bool數(shù)組,用來標(biāo)識是否已經(jīng)訪問過該節(jié)點。
第一步:首先我們從isTrav數(shù)組中選出一個未被訪問的節(jié)點,如V1。
第二步:訪問V1的鄰接點V2,V3,V5,并將這三個節(jié)點標(biāo)記為true。
第三步:第二步結(jié)束后,我們開始訪問V2的鄰接點V1,V3,但是他們都是被訪問過的。
第四步:我們從第二步結(jié)束的V3出發(fā)訪問他的鄰接點V2,V1,V5,V4,還好V4是未被訪問的,此時標(biāo)記一下。
第五步:我們訪問V5的鄰接點V1,V3,V4,不過都是已經(jīng)訪問過的。
第六步:有的圖中通過一個頂點的“廣度優(yōu)先”不能遍歷所有的頂點,此時我們重復(fù)(1-5)的步驟就可以最終完成廣度優(yōu)先遍歷。

復(fù)制代碼 代碼如下:
#region 廣度優(yōu)先
/// summary>
/// 廣度優(yōu)先
/// /summary>
/// param name="graph">/param>
public void BFSTraverse(MatrixGraph graph)
{
//訪問標(biāo)記默認初始化
for (int i = 0; i graph.vertexNum; i++)
{
graph.isTrav[i] = false;
}
//遍歷每個頂點
for (int i = 0; i graph.vertexNum; i++)
{
//廣度遍歷未訪問過的頂點
if (!graph.isTrav[i])
{
BFSM(ref graph, i);
}
}
}
/// summary>
/// 廣度遍歷具體算法
/// /summary>
/// param name="graph">/param>
public void BFSM(ref MatrixGraph graph, int vertex)
{
//這里就用系統(tǒng)的隊列
Queueint> queue = new Queueint>();
//先把頂點入隊
queue.Enqueue(vertex);
//標(biāo)記此頂點已經(jīng)被訪問
graph.isTrav[vertex] = true;
//輸出頂點
Console.Write(" ->" + graph.vertex[vertex]);
//廣度遍歷頂點的鄰接點
while (queue.Count != 0)
{
var temp = queue.Dequeue();
//遍歷矩陣的橫坐標(biāo)
for (int i = 0; i graph.vertexNum; i++)
{
if (!graph.isTrav[i] graph.edges[temp, i] != 0)
{
graph.isTrav[i] = true;
queue.Enqueue(i);
//輸出未被訪問的頂點
Console.Write(" ->" + graph.vertex[i]);
}
}
}
}
#endregion
3> 深度優(yōu)先
同樣是這個圖,大家看看如何實現(xiàn)深度優(yōu)先,深度優(yōu)先就像鐵骨錚錚的好漢,遵循“能進則進,不進則退”的原則。
第一步:同樣也是從isTrav數(shù)組中選出一個未被訪問的節(jié)點,如V1。
第二步:然后一直訪問V1的鄰接點,一直到走頭無路的時候“回溯”,路線為V1,V2,V3,V4,V5,到V5的時候訪問鄰接點V1,發(fā)現(xiàn)V1是訪問過的,
此時一直回溯的訪問直到V1。
第三步: 同樣有的圖中通過一個頂點的“深度優(yōu)先”不能遍歷所有的頂點,此時我們重復(fù)(1-2)的步驟就可以最終完成深度優(yōu)先遍歷。

復(fù)制代碼 代碼如下:
#region 深度優(yōu)先
/// summary>
/// 深度優(yōu)先
/// /summary>
/// param name="graph">/param>
public void DFSTraverse(MatrixGraph graph)
{
//訪問標(biāo)記默認初始化
for (int i = 0; i graph.vertexNum; i++)
{
graph.isTrav[i] = false;
}
//遍歷每個頂點
for (int i = 0; i graph.vertexNum; i++)
{
//廣度遍歷未訪問過的頂點
if (!graph.isTrav[i])
{
DFSM(ref graph, i);
}
}
}
#region 深度遞歸的具體算法
/// summary>
/// 深度遞歸的具體算法
/// /summary>
/// param name="graph">/param>
/// param name="vertex">/param>
public void DFSM(ref MatrixGraph graph, int vertex)
{
Console.Write("->" + graph.vertex[vertex]);
//標(biāo)記為已訪問
graph.isTrav[vertex] = true;
//要遍歷的六個點
for (int i = 0; i graph.vertexNum; i++)
{
if (graph.isTrav[i] == false graph.edges[vertex, i] != 0)
{
//深度遞歸
DFSM(ref graph, i);
}
}
}
#endregion
#endregion
最后上一下總的代碼
復(fù)制代碼 代碼如下:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace MatrixGraph
{
public class Program
{
static void Main(string[] args)
{
MatrixGraphManager manager = new MatrixGraphManager();
//創(chuàng)建圖
MatrixGraph graph = manager.CreateMatrixGraph();
manager.OutMatrix(graph);
Console.Write("廣度遞歸:\t");
manager.BFSTraverse(graph);
Console.Write("\n深度遞歸:\t");
manager.DFSTraverse(graph);
Console.ReadLine();
}
}
#region 鄰接矩陣的結(jié)構(gòu)圖
/// summary>
/// 鄰接矩陣的結(jié)構(gòu)圖
/// /summary>
public class MatrixGraph
{
//保存頂點信息
public string[] vertex;
//保存邊信息
public int[,] edges;
//深搜和廣搜的遍歷標(biāo)志
public bool[] isTrav;
//頂點數(shù)量
public int vertexNum;
//邊數(shù)量
public int edgeNum;
//圖類型
public int graphType;
/// summary>
/// 存儲容量的初始化
/// /summary>
/// param name="vertexNum">/param>
/// param name="edgeNum">/param>
/// param name="graphType">/param>
public MatrixGraph(int vertexNum, int edgeNum, int graphType)
{
this.vertexNum = vertexNum;
this.edgeNum = edgeNum;
this.graphType = graphType;
vertex = new string[vertexNum];
edges = new int[vertexNum, vertexNum];
isTrav = new bool[vertexNum];
}
}
#endregion
/// summary>
/// 圖的操作類
/// /summary>
public class MatrixGraphManager
{
#region 圖的創(chuàng)建
/// summary>
/// 圖的創(chuàng)建
/// /summary>
/// param name="g">/param>
public MatrixGraph CreateMatrixGraph()
{
Console.WriteLine("請輸入創(chuàng)建圖的頂點個數(shù),邊個數(shù),是否為無向圖(0,1來表示),已逗號隔開。");
var initData = Console.ReadLine().Split(',').Select(i => int.Parse(i)).ToList();
MatrixGraph graph = new MatrixGraph(initData[0], initData[1], initData[2]);
Console.WriteLine("請輸入各頂點信息:");
for (int i = 0; i graph.vertexNum; i++)
{
Console.Write("\n第" + (i + 1) + "個頂點為:");
var single = Console.ReadLine();
//頂點信息加入集合中
graph.vertex[i] = single;
}
Console.WriteLine("\n請輸入構(gòu)成兩個頂點的邊和權(quán)值,以逗號隔開。\n");
for (int i = 0; i graph.edgeNum; i++)
{
Console.Write("第" + (i + 1) + "條邊:\t");
initData = Console.ReadLine().Split(',').Select(j => int.Parse(j)).ToList();
int start = initData[0];
int end = initData[1];
int weight = initData[2];
//給矩陣指定坐標(biāo)位置賦值
graph.edges[start - 1, end - 1] = weight;
//如果是無向圖,則數(shù)據(jù)呈“二,四”象限對稱
if (graph.graphType == 1)
{
graph.edges[end - 1, start - 1] = weight;
}
}
return graph;
}
#endregion
#region 輸出矩陣數(shù)據(jù)
/// summary>
/// 輸出矩陣數(shù)據(jù)
/// /summary>
/// param name="graph">/param>
public void OutMatrix(MatrixGraph graph)
{
for (int i = 0; i graph.vertexNum; i++)
{
for (int j = 0; j graph.vertexNum; j++)
{
Console.Write(graph.edges[i, j] + "\t");
}
//換行
Console.WriteLine();
}
}
#endregion
#region 廣度優(yōu)先
/// summary>
/// 廣度優(yōu)先
/// /summary>
/// param name="graph">/param>
public void BFSTraverse(MatrixGraph graph)
{
//訪問標(biāo)記默認初始化
for (int i = 0; i graph.vertexNum; i++)
{
graph.isTrav[i] = false;
}
//遍歷每個頂點
for (int i = 0; i graph.vertexNum; i++)
{
//廣度遍歷未訪問過的頂點
if (!graph.isTrav[i])
{
BFSM(ref graph, i);
}
}
}
/// summary>
/// 廣度遍歷具體算法
/// /summary>
/// param name="graph">/param>
public void BFSM(ref MatrixGraph graph, int vertex)
{
//這里就用系統(tǒng)的隊列
Queueint> queue = new Queueint>();
//先把頂點入隊
queue.Enqueue(vertex);
//標(biāo)記此頂點已經(jīng)被訪問
graph.isTrav[vertex] = true;
//輸出頂點
Console.Write(" ->" + graph.vertex[vertex]);
//廣度遍歷頂點的鄰接點
while (queue.Count != 0)
{
var temp = queue.Dequeue();
//遍歷矩陣的橫坐標(biāo)
for (int i = 0; i graph.vertexNum; i++)
{
if (!graph.isTrav[i] graph.edges[temp, i] != 0)
{
graph.isTrav[i] = true;
queue.Enqueue(i);
//輸出未被訪問的頂點
Console.Write(" ->" + graph.vertex[i]);
}
}
}
}
#endregion
#region 深度優(yōu)先
/// summary>
/// 深度優(yōu)先
/// /summary>
/// param name="graph">/param>
public void DFSTraverse(MatrixGraph graph)
{
//訪問標(biāo)記默認初始化
for (int i = 0; i graph.vertexNum; i++)
{
graph.isTrav[i] = false;
}
//遍歷每個頂點
for (int i = 0; i graph.vertexNum; i++)
{
//廣度遍歷未訪問過的頂點
if (!graph.isTrav[i])
{
DFSM(ref graph, i);
}
}
}
#region 深度遞歸的具體算法
/// summary>
/// 深度遞歸的具體算法
/// /summary>
/// param name="graph">/param>
/// param name="vertex">/param>
public void DFSM(ref MatrixGraph graph, int vertex)
{
Console.Write("->" + graph.vertex[vertex]);
//標(biāo)記為已訪問
graph.isTrav[vertex] = true;
//要遍歷的六個點
for (int i = 0; i graph.vertexNum; i++)
{
if (graph.isTrav[i] == false graph.edges[vertex, i] != 0)
{
//深度遞歸
DFSM(ref graph, i);
}
}
}
#endregion
#endregion
}
}
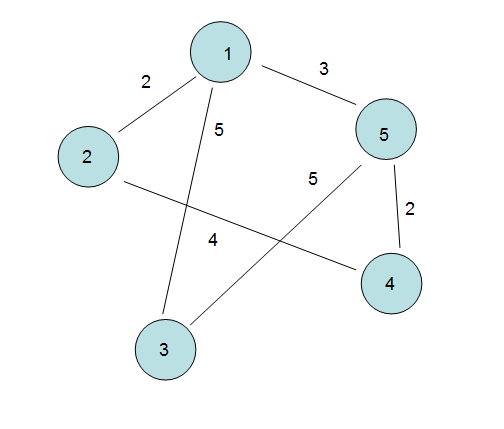
代碼中我們構(gòu)建了如下的“圖”。
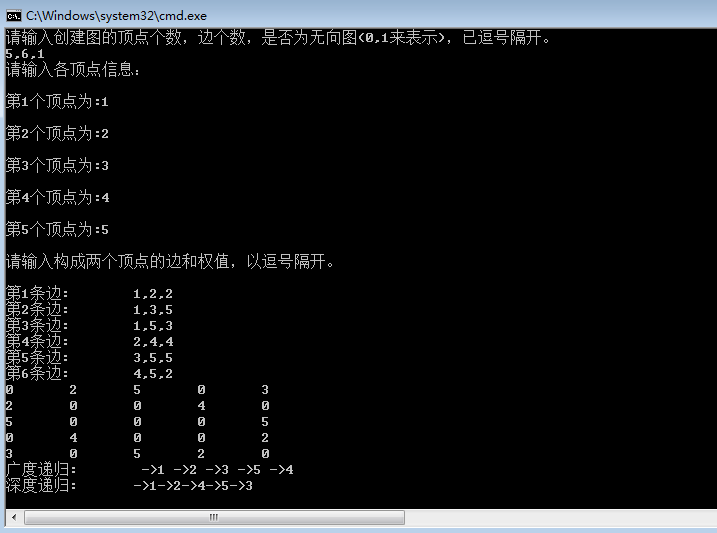
您可能感興趣的文章:- 算法系列15天速成——第十三天 樹操作【下】
- 算法系列15天速成 第十二天 樹操作【中】
- 算法系列15天速成 第十一天 樹操作(上)
- 算法系列15天速成 第十天 棧
- 算法系列15天速成 第八天 線性表【下】
- 算法系列15天速成 第九天 隊列
- 算法系列15天速成 第七天 線性表【上】
- 算法系列15天速成 第六天 五大經(jīng)典查找【下】
- 算法系列15天速成 第五天 五大經(jīng)典查找【中】
- 算法系列15天速成 第四天 五大經(jīng)典查找【上】
- 算法系列15天速成 第三天 七大經(jīng)典排序【下】
- 算法系列15天速成 第二天 七大經(jīng)典排序【中】
- 算法系列15天速成 第一天 七大經(jīng)典排序【上】
- 算法系列15天速成——第十五天 圖【下】(大結(jié)局)