冒泡排序
冒泡排序是一種簡(jiǎn)單的排序算法。它重復(fù)地走訪過(guò)要排序的數(shù)列,一次比較兩個(gè)元素,如果它們的順序錯(cuò)誤就把它們交換過(guò)來(lái)。走訪數(shù)列的工作是重復(fù)地進(jìn)行直到?jīng)]有再需要交換,也就是說(shuō)該數(shù)列已經(jīng)排序完成。這個(gè)算法的名字由來(lái)是因?yàn)樵叫〉脑貢?huì)經(jīng)由交換慢慢“浮”到數(shù)列的頂端。
def mao(lst):
for i in range(len(lst)):
# 由于每一輪結(jié)束后,總一定有一個(gè)大的數(shù)排在后面
# 而且后面的數(shù)已經(jīng)排好了
# 即i輪之后,就有i個(gè)數(shù)字被排好
# 所以其 len-1 -i到 len-1的位置是已經(jīng)排好的了
# 只需要比較0到len -1 -i的位置即可
# flag 用于標(biāo)記是否剛開(kāi)始就是排好的數(shù)據(jù)
# 只有當(dāng)flag狀態(tài)發(fā)生改變時(shí)(第一次循環(huán)就可以確定),繼續(xù)排序,否則返回
flag = False
for j in range(len(lst) - i - 1):
if lst[j] > lst[j + 1]:
lst[j], lst[j + 1] = lst[j + 1], lst[j]
flag = True
# 非排好的數(shù)據(jù),改變flag
if not flag:
return lst
return lst
print(mao([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
選擇排序
選擇排序是一種簡(jiǎn)單直觀的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再?gòu)氖S辔磁判蛟刂欣^續(xù)尋找最小(大)元素,然后放到已排序序列的末尾。以此類(lèi)推,直到所有元素均排序完畢。
# 選擇排序是從前開(kāi)始排的
# 選擇排序是從一個(gè)列表中找出一個(gè)最小的元素,然后放在第一位上。
# 冒泡排序類(lèi)似
# 其 0 到 i的位置是排好的,只需要排i+1到len(lst)-1即可
def select_sort(lst):
for i in range(len(lst)):
min_index = i # 用于記錄最小的元素的索引
for j in range(i + 1, len(lst)):
if lst[j] lst[min_index]:
min_index = j
# 此時(shí),已經(jīng)確定,min_index為 i+1 到len(lst) - 1 這個(gè)區(qū)間最小值的索引
lst[i], lst[min_index] = lst[min_index], lst[i]
return lst
def select_sort2(lst):
# 第二種選擇排序的方法
# 原理與第一種一樣
# 不過(guò)不需要引用中間變量min_index
# 只需要找到索引i后面的i+1到len(lst)的元素即可
for i in range(len(lst)):
for j in range(len(lst) - i):
# lst[i + j]是一個(gè)i到len(lst)-1的一個(gè)數(shù)
# 因?yàn)閖 = len(lst) -i 即 j + i = len(lst)
if lst[i] > lst[i + j]:
# 說(shuō)明后面的數(shù)更小,更換位置
lst[i], lst[i + j] = lst[i + j], lst[i]
return lst
print(select_sort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
print(select_sort2([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
快速排序
快速排序是通過(guò)一趟排序?qū)⒋庞涗浄指舫瑟?dú)立的兩部分,其中一部分記錄的關(guān)鍵字均比另一部分的關(guān)鍵字小,則可分別對(duì)這兩部分記錄繼續(xù)進(jìn)行排序,以達(dá)到整個(gè)序列有序。
# 原理
# 1. 任取列表中的一個(gè)元素i
# 2. 把列表中大于i的元素放于其右邊,小于則放于其左邊
# 3. 如此重復(fù)
# 4. 直到不能在分,即只剩1個(gè)元素了
# 5. 然后將這些結(jié)果組合起來(lái)
def quicksort(lst):
if len(lst) 2: # lst有可能為空
return lst
# ['pɪvət] 中心點(diǎn)
pivot = lst[0]
less_lst = [i for i in lst[1:] if i = pivot]
greater_lst = [i for i in lst[1:] if i > pivot]
# 最后的結(jié)果就是
# 左邊的結(jié)果 + 中間值 + 右邊的結(jié)果
# 然后細(xì)分 左+中+右 + 中間值 + 左 + 中+ 右
# ........... + 中間值 + ............
return quicksort(less_lst) + [pivot] + quicksort(greater_lst)
print(quicksort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
print(quicksort([1, 5, 8, 62]))
插入排序
插入排序的算法描述是一種簡(jiǎn)單直觀的排序算法。它的工作原理是通過(guò)構(gòu)建有序序列,對(duì)于未排序數(shù)據(jù),在已排序序列中從后向前掃描,找到相應(yīng)位置并插入。
# lst的[0, i) 項(xiàng)是有序的,因?yàn)橐呀?jīng)排過(guò)了
# 那么只需要比對(duì)第i項(xiàng)的lst[i]和lst[0 : i]的元素大小即可
# 假如,lst[i]大,則不用改變位置
# 否則,lst[i]改變位置,插到j(luò)的位置,而lst[j]自然往后挪一位
# 然后再刪除lst[i+1]即可(lst[i+1]是原來(lái)的lst[i])
#
# 重復(fù)上面步驟即可,排序完成
def insert_sort(lst: list):
# 外層開(kāi)始的位置從1開(kāi)始,因?yàn)閺?開(kāi)始都沒(méi)得排
# 只有兩個(gè)元素以上才能排序
for i in range(1, len(lst)):
# 內(nèi)層需要從0開(kāi)始,因?yàn)閘st[0]的位置不一定是最小的
for j in range(i):
if lst[i] lst[j]:
lst.insert(j, lst[i])
# lst[i]已經(jīng)插入到j(luò)的位置了,j之后的元素都往后+1位,所以刪除lst[i+1]
del lst[i + 1]
return lst
print(insert_sort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
希爾排序
希爾排序是1959年Shell發(fā)明的,第一個(gè)突破O(n2)的排序算法,是簡(jiǎn)單插入排序的改進(jìn)版。它與插入排序的不同之處在于,它會(huì)優(yōu)先比較距離較遠(yuǎn)的元素。希爾排序又叫縮小增量排序。
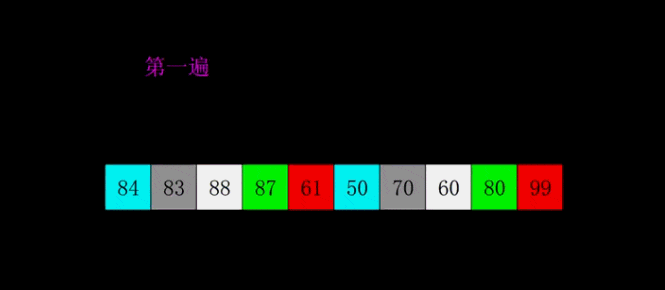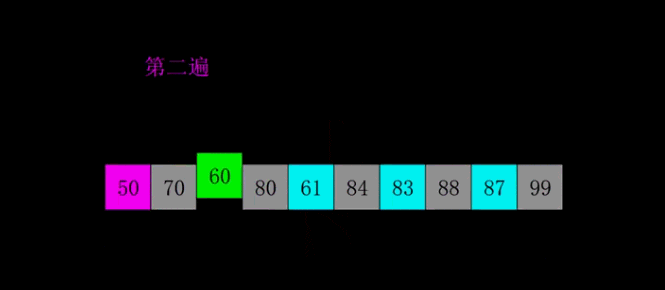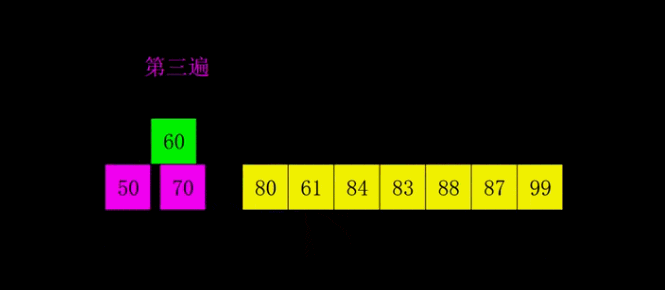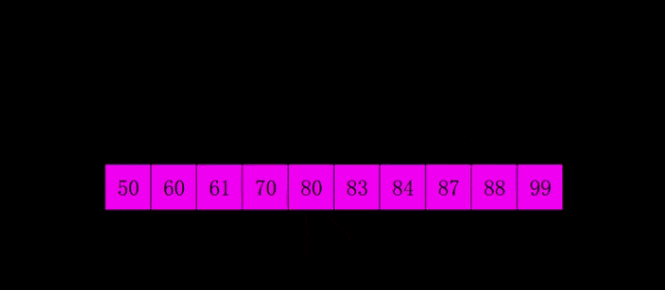
希爾排序
# 希爾排序是對(duì)直接插入排序的優(yōu)化版本
# 1. 分組:
# 每間隔一段距離取一個(gè)元素為一組
# 間隔自己確定,一般為lst的一半
# 2. 根據(jù)插入排序,把每一組排序好
# 3. 繼續(xù)分組:
# 同樣沒(méi)間隔一段距離取一個(gè)元素為一組
# 間隔要求比 之前的間隔少一半
# 4. 再每組插入排序
# 5. 直到間隔為1,則排序完成
#
def shell_sort(lst):
lst_len = len(lst)
gap = lst_len // 2 # 整除2,取間隔
while gap >= 1: # 間隔為0時(shí)結(jié)束
for i in range(gap, lst_len):
temp = lst[i]
j = i
# 插入排序
while j - gap >= 0 and lst[j - gap] > temp:
lst[j] = lst[j - gap]
j -= gap
lst[j] = temp
gap //= 2
return lst
print(shell_sort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
# 奇數(shù)
# gap = 2
# [5, 2, 4, 3, 1]
# [5, 4, 1] [2, 3]
# [1, 4, 5, 2, 3]
# gap = 1
# [1, 2, 3, 4, 5]
# 偶數(shù)
# gap = 3
# [5, 2, 4, 3, 1, 6]
# [5, 3] [2, 1] [4,6]
# [3, 5, 1, 2, 4 , 6]
# gap = 1
# [1, 2, 3, 4, 5, 6]
并歸排序
歸并排序是建立在歸并操作上的一種有效的排序算法。該算法是采用分治法(Divide and Conquer)的一個(gè)非常典型的應(yīng)用。將已有序的子序列合并,得到完全有序的序列;即先使每個(gè)子序列有序,再使子序列段間有序。若將兩個(gè)有序表合并成一個(gè)有序表,稱(chēng)為2-路歸并。
并歸排序
# 利用分治法
# 不斷將lst分為左右兩個(gè)分
# 直到不能再分
# 然后返回
# 將兩邊的列表的元素進(jìn)行比對(duì),排序然后返回
# 不斷重復(fù)上面這一步驟
# 直到排序完成,即兩個(gè)大的列表比對(duì)完成
def merge(left, right):
# left 可能為只有一個(gè)元素的列表,或已經(jīng)排好序的多個(gè)元素列表(之前調(diào)用過(guò)merge)
# right 也一樣
res = []
while left and right:
item = left.pop(0) if left[0] right[0] else right.pop(0)
res.append(item)
# 此時(shí),left或right已經(jīng)有一個(gè)為空,直接extend插入
# 而且,left和right是之前已經(jīng)排好序的列表,不需要再操作了
res.extend(left)
res.extend(right)
return res
def merge_sort(lst):
lst_len = len(lst)
if lst_len = 1:
return lst
mid = lst_len // 2
lst_right = merge_sort(lst[mid:len(lst)]) # 返回的時(shí)lst_len = 1時(shí)的 lst 或 merge中進(jìn)行排序后的列表
lst_left = merge_sort(lst[:mid]) # 返回的是lst_len = 1時(shí)的 lst 或 merge中進(jìn)行排序后的列表
return merge(lst_left, lst_right) # 進(jìn)行排序,lst_left lst_right 的元素會(huì)不斷增加
print(merge_sort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
堆排序
堆排序是指利用堆這種數(shù)據(jù)結(jié)構(gòu)所設(shè)計(jì)的一種排序算法。堆積是一個(gè)近似完全二叉樹(shù)的結(jié)構(gòu),并同時(shí)滿足堆積的性質(zhì):即子結(jié)點(diǎn)的鍵值或索引總是小于(或者大于)它的父節(jié)點(diǎn)。然后進(jìn)行排序。

堆排序
# 把列表創(chuàng)成一個(gè)大根堆或小根堆
# 然后根據(jù)大(小)根堆的特點(diǎn):根節(jié)點(diǎn)最大(小),逐一取值
#
# 升序----使用大頂堆
#
# 降序----使用小頂堆
# 本例以小根堆為例
# 列表lst = [1, 22 ,11, 8, 12, 4, 9]
# 1. 建成一個(gè)普通的堆:
# 1
# / \
# 22 11
# / \ / \
# 8 12 4 9
#
# 2. 進(jìn)行調(diào)整,從子開(kāi)始調(diào)整位置,要求: 父節(jié)點(diǎn)= 字節(jié)點(diǎn)
#
# 1 1 1
# / \ 13和22調(diào)換位置 / \ 4和11調(diào)換位置 / \
# 22 11 ==============> 13 11 ==============> 13 4
# / \ / \ / \ / \ / \ / \
# 13 14 4 9 22 14 4 9 22 14 11 9
#
# 3. 取出樹(shù)上根節(jié)點(diǎn),即最小值,把換上葉子節(jié)點(diǎn)的最大值
#
# 1
# /
# ~~~~/
# 22
# / \
# 8 4
# \ / \
# 12 11 9
#
# 4. 按照同樣的道理,繼續(xù)形成小根堆,然后取出根節(jié)點(diǎn),。。。。重復(fù)這個(gè)過(guò)程
#
# 1 1 1 4 1 4 1 4 8 1 4 8
# / / / / / /
# ~~~/ ~~~/ ~~~/ ~~~/ ~~~/ ~~~/
# 22 4 22 8 22 9
# / \ / \ / \ / \ / \ / \
# 8 4 8 9 8 9 12 9 12 9 12 11
# \ / \ \ / \ \ / \ / / /
# 12 11 9 12 11 22 12 11 22 11 11 22
#
# 續(xù)上:
# 1 4 8 9 1 4 8 9 1 4 8 9 11 1 4 8 9 11 1 4 8 9 11 12 ==> 1 4 8 9 11 12 22
# / / / / /
# ~~~/ ~~~/ ~~~/ ~~~/ ~~~/
# 22 11 22 12 22
# / \ / \ / /
# 12 11 12 22 12 22
#
# 代碼實(shí)現(xiàn)
def heapify(lst, lst_len, i):
"""創(chuàng)建一個(gè)堆"""
less = i # largest為最大元素的索引
left_node_index = 2 * i + 1 # 左子節(jié)點(diǎn)索引
right_node_index = 2 * i + 2 # 右子節(jié)點(diǎn)索引
# lst[i] 就是父節(jié)點(diǎn)(假如有子節(jié)點(diǎn)的話):
#
# lst[i]
# / \
# lst[2*i + 1] lst[ 2*i + 2]
#
# 想要大根堆,即升序, 將判斷左右子節(jié)點(diǎn)大小的 ‘>' 改為 ‘' 即可
#
if left_node_index lst_len and lst[less] > lst[left_node_index]:
less = left_node_index
if right_node_index lst_len and lst[less] > lst[right_node_index]:
# 右邊節(jié)點(diǎn)最小的時(shí)候
less = right_node_index
if less != i:
# 此時(shí),是字節(jié)點(diǎn)大于父節(jié)點(diǎn),所以相互交換位置
lst[i], lst[less] = lst[less], lst[i] # 交換
heapify(lst, lst_len, less)
# 節(jié)點(diǎn)變動(dòng)了,需要再檢查一下
def heap_sort(lst):
res = []
i = len(lst)
lst_len = len(lst)
for i in range(lst_len, -1, -1):
# 要從葉節(jié)點(diǎn)開(kāi)始比較,所以倒著來(lái)
heapify(lst, lst_len, i)
# 此時(shí),已經(jīng)建好了一個(gè)小根樹(shù)
# 所以,交換元素,將根節(jié)點(diǎn)(最小值)放在后面,重復(fù)這個(gè)過(guò)程
for j in range(lst_len - 1, 0, -1):
lst[0], lst[j] = lst[j], lst[0] # 交換,最小的放在j的位置
heapify(lst, j, 0) # 再次構(gòu)建一個(gè)[0: j)小根堆 [j: lst_len-1]已經(jīng)倒序排好了
return lst
arr = [1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]
print(heap_sort(arr))
參考:
十大經(jīng)典排序算法(動(dòng)圖演示)
數(shù)據(jù)結(jié)構(gòu)與算法-排序篇-Python描述
動(dòng)圖可以點(diǎn)擊這里查看
我的github
我的博客
我的筆記
到此這篇關(guān)于python3實(shí)現(xiàn)常見(jiàn)的排序算法(示例代碼)的文章就介紹到這了,更多相關(guān)python排序算法內(nèi)容請(qǐng)搜索腳本之家以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持腳本之家!
您可能感興趣的文章:- 新手初學(xué)Java常見(jiàn)排序算法
- JavaScript實(shí)現(xiàn)的七種排序算法總結(jié)(推薦!)
- 優(yōu)化常見(jiàn)的java排序算法
- java排序算法圖文詳解
- 常見(jiàn)的排序算法,一篇就夠了